La navigazione astronomica tradizionale
Ora impareremo a trovare il punto nave con un metodo tradizionale che non si avvale né del computer né della calcolatrice programmabile, bensì del carteggio e delle Effemeridi Nautiche; tuttavia, per risolvere i calcoli trigonometrici e per evitare possibili errori, useremo inizialmente una calcolatrice al posto delle tavole dei logaritmi per trovare il seno, il coseno, la tangente etc. e per eseguire le quattro operazioni. Calcolatrici tascabili con queste funzioni sono disponibili nei reparti scolastici di quasi tutti i grandi magazzini per poco più di una decina di euro; conviene scegliere un modello che lavori in gradi e non in radianti (vedremo più avanti come si fa ad accorgersene con una semplicissima prova) e che offra la trasformazione dei gradi sessagesimali in gradi decimali, quindi che sappia trasformare, per esempio, 32° 30' in 32,5°.
Chi volesse fare a meno anche della calcolatrice ed avvalersi solo di carta e penna può utilizzare le tavole a soluzione diretta H.O.214 pubblicate in Italia dall’Istituto Idrografico della Marina. Tuttavia si consiglia, almeno la prima volta, di seguire il metodo con la calcolatrice illustrato nelle prossime pagine, in quanto didatticamente molto valido per apprendere il procedimento e capire cosa si sta calcolando. L’uso delle H.O.214, è invece più meccanico e meno ragionato: c’è il rischio di arrivare alla soluzione senza avere compreso cosa si è fatto, ma dà la soddisfazione di trovare il punto nave senza alcun ausilio elettronico.
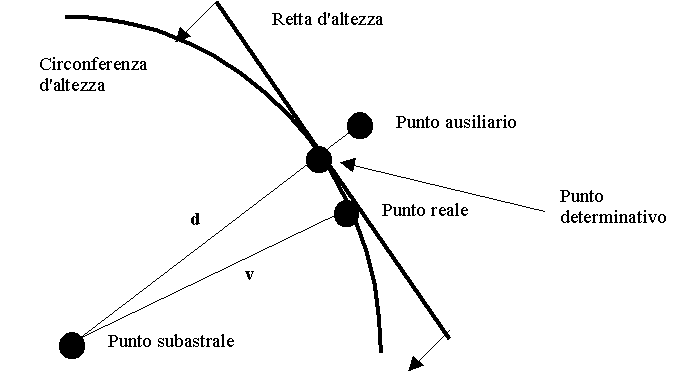
Ripassiamo il concetto, già illustrato, di retta d'altezza. Si tratta dell'approssimazione della circonferenza d'altezza in una retta, in prossimità dell'osservatore. Il procedimento presuppone quindi la conoscenza delle nostre coordinate approssimate. Ecco perché la conoscenza del punto stimato diviene estremamente più importante rispetto al sistema delle circonferenze: le sue coordinate dovranno essere il più precise possibile. Nella ricerca della retta d'altezza il punto stimato viene anche chiamato punto ausiliario.
Cosa sono ed a cosa servono le Effemeridi Nautiche? Sono una pubblicazione edita annualmente dall'Istituto Idrografico della Marina. Contiene i dati sui corpi celesti validi per l'anno in corso necessari per la navigazione astronomica, insieme all'indicazione di alcuni fenomeni, come le eclissi.
Il corpo principale del volume consiste in un elenco delle coordinate dei pianeti visibili ad occhio nudo (Mercurio escluso), della Luna e del Sole, aggiornate ora per ora. Le coordinate presentate sono l'angolo orario e la declinazione apparente dell'astro, che corrispondono alla longitudine (partendo dal meridiano di Greenwich in direzione Ovest) ed alla latitudine dei punti subastrali. Viene poi indicato il Tempo Siderale, aggiornato anch'esso ora per ora. Per le 66 stelle di uso nautico invece sono riportate la coascensione retta e la declinazione, aggiornate ogni tre giorni, in quanto questi valori per le stelle variano molto lentamente. Sommando la coascensione retta al Tempo Siderale (che è aggiornato ora per ora), si ottiene anche per le stelle la longitudine da Greenwich in senso Ovest; quindi anche per le stelle si ottengono, con una semplice addizione, le coordinate dei loro punti subastrali ora per ora. Ogni pagina contiene i dati relativi a tre giorni, contenendo 72 righe per i pianeti, la Luna, il Sole ed il Tempo Siderale, e 66 righe per le singole stelle.
Mercurio non viene preso in considerazione, in quanto essendo sempre piuttosto vicino al Sole, molto difficilmente è visibile ad un'altezza tale da renderlo utilizzabile per la navigazione astronomica.
L'ultima parte delle Effemeridi Nautiche, quella con le pagine colorate, contiene le tabelle per interpolare i dati forniti nel corpo centrale e per apportare le correzioni all'altezza misurata col sestante per la rifrazione, la parallasse, l'altezza sull'orizzonte ed il semidiametro.
Le Effemeridi Nauitiche non sono l'unica pubblicazione italiana da cui si possano ricavare le coordinate dei punti subastrali. Esiste anche l'ottimo e già citato "Almanacco Astronomico e Nautico" di S. De Meis e J. Meeus, attualmente edito da Mimesis: è molto più interessante in quanto fornisce praticamente tutti i fenomeni astronomici dell'anno in corso che possano interessare l'astrofilo, costa considerevolmente meno ed è più diffuso (si trova anche nelle migliori edicole). Contiene le indicazioni per correggere le altezze ed è quindi uno strumento completo; per contro ritengo che sia più macchinoso per ricavare i dati dei punti subastrali: una calcolatrice è d'obbligo. Qui spiegheremo soltanto come utilizzare le Effemeridi Nautiche, in quanto è la pubblicazione che viene tradizionalmente usata per la navigazione astronomica.
Come si ricava la retta d'altezza
Abbiamo visto in quest'Appendice come l'altezza di un astro sull'orizzonte fornisca la distanza tra l'osservatore ed il punto subastrale. Più precisamente, un'altezza di 89° significa una distanza di un grado dal punto subastrale. Un'altezza di 88° una distanza di due gradi e così via. In parole povere, l'angolo complementare all'altezza indica la distanza in gradi dal punto subastrale. Ma un grado corrisponde a 60 primi ed un primo di grado corrisponde ad una distanza sulla superficie terrestre di un miglio nautico. Possiamo quindi dire che la distanza in miglia nautiche fra la posizione reale dell'osservatore ed il punto subastrale corrisponde all'angolo complementare all'altezza dell'astro sull'orizzonte moltiplicato per 60.
In parole povere, col sestante possiamo ricavare la nostra distanza vera dal punto subastrale.
Il secondo passaggio consiste nel ricavare la distanza fra il punto ausiliario ed il punto subastrale: è un passaggio esclusivamente matematico.
Il terzo passaggio consiste nel ricavare l'azimuth fra il punto ausiliario ed il punto subastrale, ossia la direzione, partendo dal Nord vero, fra il punto ausiliario ed il punto subastrale.
Diamo uno sguardo al seguente disegno:

Chiamiamo v la distanza dal punto vero al punto subastrale, ricavata dal sestante, d la distanza dal punto ausiliario al punto subastrale, calcolata matematicamente, a l'azimuth dal punto ausiliario al punto subastrale, calcolato anch'esso matematicamente. Calcoliamo d - v. Se questa quantità è positiva, ossia se la distanza fra il punto ausiliario ed il punto subastrale è più grande della distanza fra il punto vero ed il punto subastrale, siamo nel caso appena disegnato. Allora partendo dal punto ausiliario in direzione a per un tratto lungo d - v, arriviamo nel punto determinativo. Da questo punto tracciamo una retta di azimuth perpendicolare ad a; è la nostra retta d'altezza cercata. All'estremità della retta d'altezza è buona norma tracciare due frecce perpendicolari che indichino la direzione del punto subastrale
Se viceversa v - d fosse una quantità negativa, ossia se la distanza fra il punto ausiliario ed il punto subastrale fosse più piccola della distanza fra il punto vero ed il punto subastrale, allora il disegno da prendere in considerazione sarebbe il seguente:
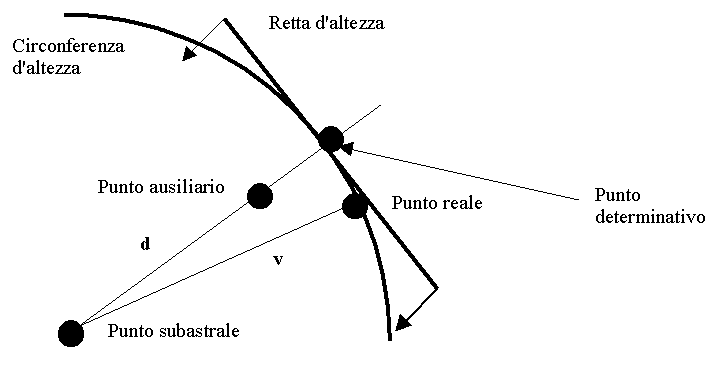
in questo caso partiamo dal punto ausiliario per una direzione a + 180° per il tratto v - d ed arriviamo nel punto determinativo. Da lì tracciamo la retta di azimuth perpendicolare ad a ed otteniamo la retta d'altezza.
Come si usano le Effemeridi Nautiche
Prima di fare degli esempi pratici un piccolo avvertimento per le operazioni con i gradi sessagesimali: ogni volta che i primi superino il valore di 60 bisogna aggiungere un'unità al valore dei gradi e sottarre 60 al valore dei primi; per esempio, 45° 43,7' + 12° 24,4' è uguale a 57° 68,1' cioè 58° 8,1'.
Vediamo ora come si trovano le coordinate di un punto subastrale. Facciamo tre esempi, con un pianeta, con la Luna e con una stella.
Vogliamo trovare la latitudine e la longitudine dei punti subastrali di Venere, della Luna e di Betelgeuse alle 4.44.41 UT del 12 settembre 1998.
Cominciamo con Venere. Apriamo le Effemeridi Nautiche alla pagina relativa a questa data, e leggiamo i dati relativi alle 4.00.00 UT. L'angolo orario (T) vale 252° 6,2'. Alla fine della colonna che riporta gli angoli orari dei tre giorni è segnato il valore della variazione oraria, v, che nel nostro caso è -0,5. Quindi andiamo nelle pagine colorate, e dal momento che che l'orario cercato è 4.44.41, andiamo alla pagina relativa ai 44 minuti. Prendiamo in considerazione la riga dei 41 secondi. La prima colonna riguarda il Sole ed i pianeti, la seconda il Tempo Siderale e la terza la Luna. Per il calcolo di Venere utilizziamo ovviamente la prima colonna, che indica 11° 10,3'. Questo è il valore che dobbiamo aggiungere all'angolo orario relativo alle ore 4.00.00 UT. Ma non è ancora finita. Dopo le prime tre colonne ce ne sono altre tre, con l'intestazione "v/d pp" (parte proporzionale della variazione) che riportano dei valori da 0 a 18 in incrementi di un decimo (sono primi di grado). Avevamo visto che il valore v posto in basso sotto la colonna trigiornaliera degli angoli orari era -0,5. Andiamo a vedere a cosa corrisponde sulla colonna "v/d pp": -0,4 (il segno era negativo). Quindi il valore dell'angolo orario di Venere relativo alle 4.44.41 del 12.9.1998 è dato da 252° 6,2' + 11° 10,3' - 0,4'. Cioè 252° 6,2' + 11° 9,9' = 263° 16,1' (è lo stesso valore che si otterrebbe col form Planetario nella colonna espressa in formato nautico). Questo è l'angolo della longitudine del punto subastrale di Venere partendo da Greenwich ed andando in verso Ovest (se il valore di v fosse stato positivo l'operazione da effettuare sarebbe stata 252° 6,2' + 11° 10,3' + 0,4'). La longitudine del punto subastrale di Venere è quindi 360° - 263° 16,1', cioè 96° 43,9' Est. Tuttavia per la determinazione della retta di altezza quest'ultimo calcolo non è necessario, in quanto lavoreremo con l'angolo orario dell'astro.
Vediamo ora come si calcola la declinazione. Alle 4.00.00 UT era di 10° 16,8' N. Il valore della variazione della declinazione, d, è posto in basso sotto la colonna della declinazione e vale -1,1 (sempre primi di grado). Andiamo nella pagina delle interpolazioni relativa ai 44 minuti e questa volta cerchiamo direttamente sulle colonne "v/d pp" il valore della sua parte proporzionale: -0,8 primi di grado (anche in questo caso il segno è negativo). Allora la declinazione è 10° 16,8' - 0,8' (sarebbe stata 10° 16,8' + 0,8' se d fosse stato positivo). La declinazione è quindi 10° 16,0' Nord (anche questo è lo stesso valore che si ottiene con Planetario). Quindi la latitudine del punto subastrale di Venere alle 4.44.41 UT del 12 settembre 1998 è 10° 16' N.
Per la Luna si opera nello stesso modo, solo che i valori v e d vengono forniti ora per ora, ed in più c'è da prendere in considerazione la parallasse, che tuttavia viene fornita direttamente e che non richiede di essere interpolata. Procedendo speditamente abbiamo che l'angolo orario vale 344° 34,2' + 10° 39,7' + 5,5' = 355° 19,4', la declinazione 16° 21,7' + 4,4' = 16° 26,1' N, la parallasse 59,1', tutti valori in perfetto accordo con quelli forniti da Planetario.
Per le stelle dobbiamo prima effettuare il calcolo del Tempo Siderale: alle 4.00.00 UT esso vale 50° 57,7'. Per il T. S. non esistono v e d, quindi si legge il valore da aggiungere direttamente sulla pagina colorata relativa a 44' 41'' (la colonna da prendere in considerazione è la seconda, quella indicata dal simbolo ¡ ), che vale 11° 12,1'. Il T. S. allora è 50° 57,7' + 11° 12,1' = 62° 9,8'.
Per il calcolo dell'angolo orario di Betelgeuse non dobbiamo fare altro che sommare la coascensione retta (colonna 360 - a ) della stella al T. S.; otteniamo quindi 271° 13,7' + 62° 9,8' = 333° 23,5'. La declinazione viene letta direttamente: 7° 24,4' Nord; anche i valori di Betelgeuse e del Tempo Siderale sono identici a quelli forniti da Planetario.
Alle ore 4.44.41 UT del 12 settembre 1998 osserviamo il lembo superiore della Luna ad un'altezza di 64° 55'. L'errore d'indice vale 1', l'altezza sull'orizzonte è di 3 metri, le coordinate del punto stimato sono 41° 0' N e 11° 0' E.
La prima cosa da fare è correggere l'altezza indicata dal sestante per l'errore d'indice. Si sottrae quest'ultimo dall'altezza: 64° 55' - 1' = 64° 54'. Se l'errore d'indice fosse stato di -1' allora l'operazione sarebbe stata 64° 55' -(-1') = 64° 55' + 1' = 64° 56'.
Le correzioni da apportare sono quelle dovute all'elevazione dell'occhio dell'osservatore sull'orizzonte, alla rifrazione atmosferica ed alla parallasse, al semidiametro (nel caso del Sole e della Luna). Le tavole per queste correzioni presenti nelle Effemeridi Nautiche hanno dei termini additivi per semplificare i calcoli. Ad esempio, per correggere un'altezza di Sole, le tavole aggiungono 20' per la correzione dell'elevazione dell'occhio, 16' per la rifrazione e la parallasse, 24' per il semidiametro. In tal modo si evitano sottrazioni, e le correzioni hanno tutte segno positivo. Solo alla fine andrà sottratto un grado intero, che è la somma dei tre termini additivi.
Tornando al nostro esempio correggiamo l'altezza di Luna di 64° 54'. La prima correzione riguarda l'elevazione dell'occhio sull'orizzonte di 3 metri. Essa vale 16,9' (nel caso il valore fosse stato esatto si scelga la più alta fra le due correzioni. Esempio: per 5,30 metri si sceglie 16,0' e non 15,9').
La seconda correzione è leggermente più laboriosa: si va sulla colonna dei 60° - 64° e si scelga la riga dei 50' relativa all'ultima delle cinque sestine di valori disponibili (in questo caso la prima sestina è relativa ai 60° e --', la seconda a 61° e --', la terza a 62° e --', etc.). La correzione vale 43,7'.
Per la terza correzione si utilizza la stessa colonna della seconda, quella relativa ai 60° - 64°. Scegliamo la riga relativa alla nostra parallasse di 59,1 ed otteniamo due valori. Prendiamo in considerazione quello relativo alla subcolonna S (il lembo che abbiamo misurato era il superiore) e ricaviamo 5'.
Ora sommiamo le tre correzioni: 16,9' + 43,7' + 5' = 65,6' = 1° 5,6' ed aggiungiamo questo valore all'altezza di 64° 54'. Otteniamo 65° 59,6'. Dobbiamo ora togliere il grado contenuto nei termini additivi presenti nelle tavole e ricaviamo l'altezza corretta del centro Luna alle 4.44.41 UT del 12 settembre 1998: 64° 59,6'.
Sfruttiamo questo valore per trovare il nostro punto determinativo. Un'altezza corretta del centro della Luna di 64° 59,6' vuole semplicemente dire che ci troviamo ad una distanza angolare di 90° - 64° 59,6' = 25° 0,4' dal punto subastrale lunare. Poiché un grado equivale a 60 miglia nautiche ci troviamo a 25 x 60 + 0,4 = 1500,4 miglia dal punto subastrale. E questo è un valore certo, in quanto è stato ricavato partendo da un valore reale.
Vediamo ora qual è la distanza fra il punto stimato ed il punto subastrale. Tale valore sarà, per l'appunto, un valore ipotetico, tanto più preciso quanto più il punto stimato si avvicina a quello reale.
A questo punto tiriamo fuori la nostra calcolatrice. La formula per calcolare la distanza fra il punto stimato ed il punto subastrale è la seguente:
D = 60 * Arccos [Sen(Latstim) * Sen(Decsub) + Cos(Latstim) * Cos(Decsub) * Cos(Longstim + Orarsub)]
dove
Latstim = latitudine del punto stimato, positiva se Nord
Longstim = longitudine del punto stimato, positiva se Est
Decsub = declinazione del punto subastrale, positiva se Nord
Orarsub = angolo orario del punto subastrale, sempre positivo
Sen = seno dell'angolo
Cos = coseno dell'angolo
Arccos = arcocoseno dell'angolo
D = distanza in miglia nautiche (se l'arcocoseno è espresso in gradi dec.)
* = operatore di moltiplicazione
Molte calcolatrici accettano l'argomento (il valore tra le parentesi tonde) delle funzioni trigonometriche in gradi decimali. Per trasformare i gradi sessagesimali in gradi decimali bisogna dividere la parte decimale per 60. Esempio: per calcolare sen(34° 45,6') bisogna dividere per 60 il valore di 45,6'. Otteniamo 0,76. Quindi in gradi decimali abbiamo 34,76°. Questo è il valore da immettere nella calcolatrice. Su alcune di esse bisognerà scrivere sen 34,76 ma su altre sarà necessario digitare 34,76 sen.
Qualora la calcolatrice operasse in radianti bisogna fare un'ulteriore trasformazione (spesso è presente un tasto che esegue la trasformazione automaticamente), da gradi decimali a radianti. Per fare ciò si moltiplichino i gradi decimali per 3,141593 (il valore di pi greco, p ) e si divida per 180, oppure si divida direttamente per 57,29577. In pratica 34,76° sono 0,606676 radianti. Sulla calcolatrice si scriverà sen 0,606676, oppure 0,606676 sen, a seconda del modello. Per scoprire se una calcolatrice accetta gli argomenti in radianti od in gradi decimali basta chiedere il seno di 90: se il risultato è 1 la calcolatrice accetta i gradi decimali, se è 0,893996 accetta i radianti. Se la calcolatrice funzionasse coi radianti sarà necessario moltiplicare il risultato finale di D per 57,29577 al fine di ottenere il risultato corretto.
Nel nostro caso i valori sono:
Latstim = 41
Longstim = 11
Orarsub = 355,3233°
Decsub = 16,435
Quindi la formula diventa
D = 60 * Arccos [Sen(41) * Sen(16,435) + Cos(41) * Cos(16,435) * Cos(11 + 355,3233)]
cioè
D = 60 * Arccos [0,656059 * 0,282927 + 0,754709 * 0,959141 * 0,993916]
D = 60 * Arccos [0,905085]
La funzione arcocoseno generalmente si ottiene premendo un tasto che convalida la seconda funzione del tasto coseno. Continuando abbiamo
D = 60 * 25,165266
D = 1509,9
Abbiamo finalmente trovato la distanza tra il punto stimato di coordinate 41° 0' N e 11° 0' E ed il punto subastrale lunare.
Avevamo calcolato che il punto in cui ci troviamo realmente si trova a 1500,4 miglia nautiche dal punto subastrale lunare. Quindi possiamo immaginare che esso si trovi a 1509,9 - 1500,4 = 9,5 miglia nautiche dal punto stimato. E poiché la distanza dal punto stimato è superiore a quella dal punto reale, per trovare il punto determinativo dobbiamo partire dal punto stimato ed andare verso il punto subastrale per 9,5 miglia. Per calcolare questa direzione utilizziamo la seguente formula, un po' più complessa:
A = Arctan (Numer./Denom.)
dove
Numer. = -Sen(Longstim + Orarsub)
Denom. = Tan(Dec) * Cos(Latstim) - Cos(Longstim + Orarsub) * Sin(Latstim)
Arctan = arcotangente dell'angolo
Qualora il Denom. fosse negativo al risultato finale di A bisogna aggiungere 180°. Calcoliamo ora A. Nel nostro caso abbiamo
Numer. = -Sen(11+355,3233) = -Sen(6,3233) = -0,110138
Denom. = Tan(16,435) * Cos(41) - Cos(6,3233) * Sen(41)
Denom. = 0,29498 * 0,754709 - 0,993916 * 0,656059
Denom. = -0,429443
Quindi
A = Arctan (-0,110138/-0,429443) = Arctan (0,256467)
Facendo l'arcotangente di 0,256467 (sulla nostra calcolatrice useremo la stessa tecnica dell'arcocoseno) otteniamo 14,4°. Ma poiché avevamo trovato che il Denom. era negativo dobbiamo aggiungere 180°. Quindi
A = 194,4° (valore in perfetto accordo con l'azimuth indicato da Planetario).
Quindi per trovare il punto determinativo sulla carta nautica si parte dal punto subastrale di coordinate 41° 0' N e 11° 0' E andando in direzione 194° per 9,5 miglia. Da lì tracciamo la nostra retta di altezza, che è perpendicolare all'azimuth A trovato; per cui ha orientamento 104° / 284° gradi. La retta d'altezza così ottenuta viene chiamata anche retta di Saint Hilaire.
Per il trasporto della retta di altezza si opera come già visto nel capitolo riguardante il form Sestante, ricordando che il trasporto va effettuato sia per il procedere della nave che per l'intensità della corrente. Se poi sussistono le condizioni (quasi contemporaneità delle osservazioni ed azimuth differenti di almeno 60°) si può ricavare una bisettrice d'altezza fra due rette d'altezza. In questo caso le frecce sono di aiuto. Ad esempio, confrontando queste due figure (vedere libro), apparentemente simili, vediamo come solo nella prima la differenza fra i due azimuth è superiore a 60°.
Ricordarsi che la bisettrice d'altezza passa tra le frecce che convergono o che divergono, ma mai tra le frecce che vanno nello stesso senso.
Disegno della retta d’altezza
Passiamo ora alla rappresentazione grafica della retta d’altezza. Si possono disegnare le rette direttamente sulla carta nautica, ma è meglio tracciarle su un foglio di carta separato e successivamente riportare solo i dati essenziali sulle mappe usate per la navigazione. Conviene usare un normale foglio di carta millimetrata, molto più economico e reperibile dei grafici quadrettati contenuti nei quaderni di calcolo editi dall’Istituto Idrografico della Marina. Tuttavia tenete presente che si possono usare anche i fogli di un comune quaderno a quadretti.
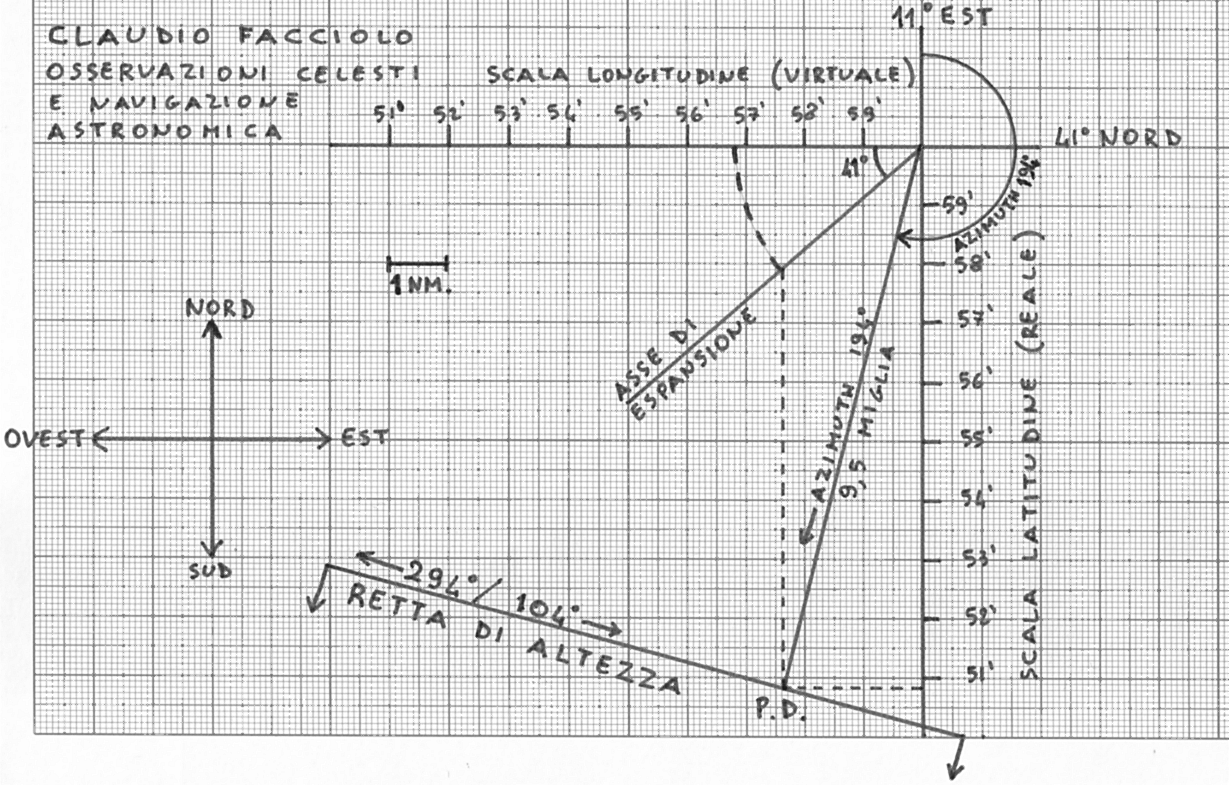
Cominciamo disegnando il parallelo ed il meridiano del punto stimato. Sul meridiano tracciamo i primi di latitudine, tenendo presente che un primo equivale ad un miglio nautico. Tracciamo sul parallelo i primi di longitudine con la stessa ampiezza: dal momento che nella realtà, a meno di non essere all’equatore, i primi di longitudine sono più stretti, abbiamo compiuto un’operazione di espansione della scala della longitudine. Tale scala è quindi virtuale. Tracciamo poi il segmento che dal punto stimato arriva al punto determinativo. Quindi tracciamo una linea dal punto stimato che intersechi il parallelo con un angolo uguale alla sua latitudine. Chiamiamo tale linea asse di espansione (può essere disegnata indifferentemente sopra o sotto il parallelo; qui l’abbiamo disegnata sotto). Leggiamo la latitudine del punto determinativo direttamente sul meridiano. Per la longitudine andiamo dal punto determinativo verso Nord fino ad intersecare l’asse di espansione. Da lì tracciamo un arco con centro nel punto stimato ed arriviamo sulla scala virtuale della longitudine.
Abbiamo così trovato che le coordinate del punto determinativo sono 40° 50,8’ N e 10° 56,8’ E.
Il procedimento appena descritto può essere eseguito anche per calcolare le coordinate di qualunque altro punto del grafico, per esempio il punto nave ottenuto dall’intersezione di due rette o di due bisettrici d’altezza.
Sul libro seguono le pagine delle Effemeridi Nautiche usate negli esempi.
Le tavole a soluzione diretta H.O. 214: il secondo metodo
Lo scopo di queste tavole è quello di fornire l'altezza vera e l'azimuth dell'astro dal punto stimato. In Italia sono pubblicate in 5 volumi dall'Istituto Idrografico della Marina col nome di I.I. 3137; il terzo volume, relativo alle latitudini da 30 a 45 gradi, è quello che si utilizza per la navigazione entro il Mediterraneo. Tuttavia occorre tenere presente che questo volume è valido sia per le latitudini da 30 a 45 gradi Nord sia per quelle tra 30 e 45 gradi Sud.
Il procedimento da seguire è illustrato all'inizio delle tavole, e vengono riportati tre metodi: la differenza fra di essi risiede esclusivamente nella scelta delle coordinate del punto stimato. Partendo dall'esempio fatto con la calcolatrice cominceremo studiando il secondo, il più naturale in quanto parte da un punto stimato che ha il valore della latitudine (e spesso, ma non necessariamente, anche della longitudine) espresso in gradi interi.
Abbiamo visto che il nostro punto stimato ha coordinate 41° 0' N e 11° 0' E. Dalle Effemeridi abbiamo poi ricavato che l'angolo orario della Luna vale 355° 19,4' e la declinazione 16° 26,1' N.
Introduciamo adesso il concetto di angolo al Polo: non è altro che la differenza di longitudine tra il punto stimato ed il punto subastrale. Ricordando per l'ennesima volta che l'angolo orario rappresenta la longitudine in senso Ovest partendo dal meridiano di Greenwich, 355° 19,4' significa una longitudine Est di 4° 40,6'. Allora nel nostro caso l'angolo al Polo P vale 11° - 4° 40,6' = 6° 19,4' (se la longitudine del punto stimato fosse stata 11° Ovest l'angolo al Polo P sarebbe stato 11° + 4° 40,6' = 15° 40,6').
Entriamo ora nelle tavole alle pagine relative a 41° di latitudine. Scegliamo quella che contiene la colonna relativa alla declinazione 16° 26,1'.
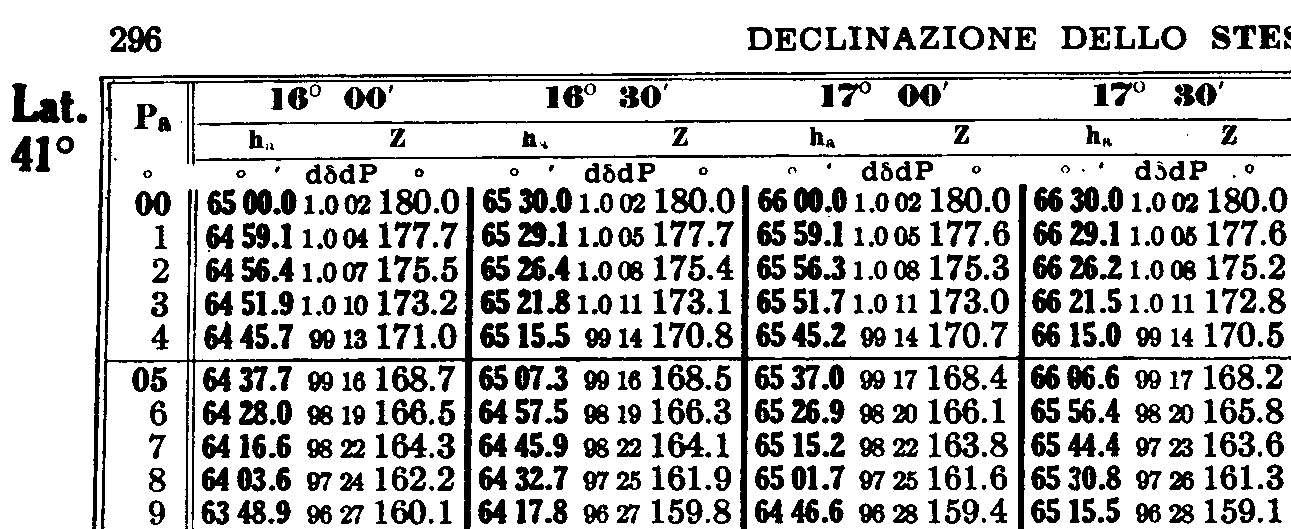
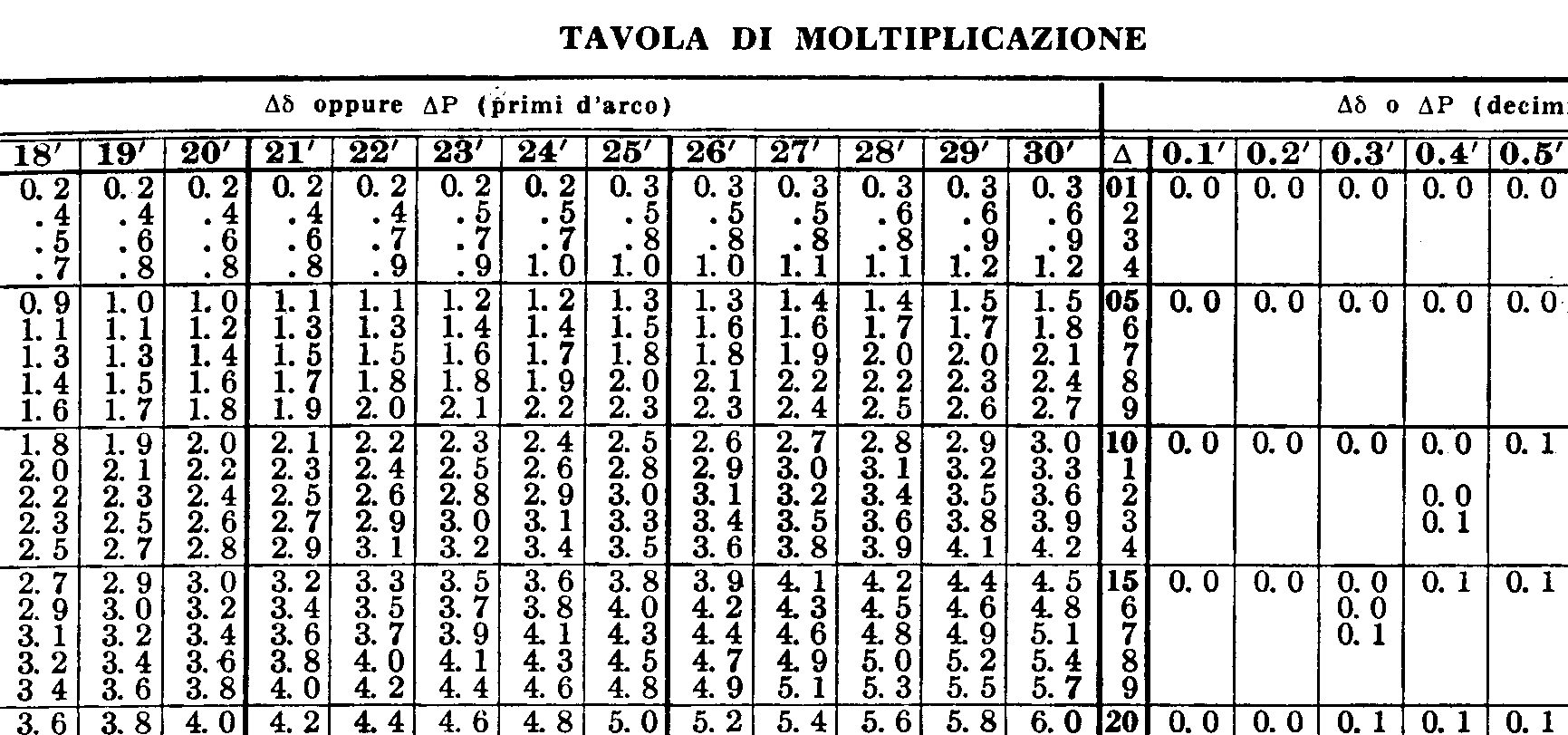
E' la pagina 296, che contiene le colonne per 16° 0' e 16° 30'. Anche la pagina 297 contiene queste due colonne, ma sono riferite a declinazioni opposte alla latitudine. Dal momento che sia la latitudine del punto stimato che la declinazione del punto subatrale hanno lo stesso nome, prendiamo in considerazione la pag. 296 (le tavole non riportano tutte le possibili declinazioni e tutti i possibili angoli P, ma solo le declinazioni a cui possono appartenere il Sole, la Luna ed i pianeti e le stelle riportate nelle Effemeridi Nautiche, e gli angoli P tali che l'altezza dell'astro non sia mai minore di 10 gradi). Guardiamo ora i valori di altezza vera e di Z, che è l'angolo (sempre compreso tra 0° e 180°) da cui ricaveremo l'azimuth, per una declinazione di 16 gradi ed angolo P di 6 gradi (ricordiamo che il nostro P vale 6° 19,4'). Otteniamo rispettivamente 64° 28,0' e 166,5°, che approssimiamo a 166. Se il punto subastrale fosse ad Est del punto stimato l'azimuth corrisponderebbe a Z. Viceversa, essendo a Ovest, come nel nostro caso, l'azimuth vale 360° - Z, cioè 194°. Tale valore, anche se approssimato, è sufficientemente preciso per i nostri scopi, e quindi non lo correggiamo ulteriormente. L'altezza va invece corretta sia per quanto riguarda la declinazione che non è esattamente di 16 gradi, sia per l'angolo P che non è esattamente di 6 gradi; la correzione per la declinazione dd vale 98 centesimi di primo. Osserviamo il valore che assume l'altezza per una declinazione di 16° 30': è maggiore, quindi la correzione per i 26,1' va assunta come positiva. Bisogna cioè aggiungere a 64° 28,0' il valore di 26,1' moltiplicato 0,98. Per fare ciò andiamo alla fine del volume, alle tavole di moltiplicazione: 26' x 0,98 vale 25,5', mentre 0,1' x 0,98 vale 0,1', quindi la correzione totale per la sola declinazione è 25,6'.

Per la correzione relativa all'angolo P si procede nello stesso modo, tuttavia poiché per un angolo P di 7 gradi il valore dell'altezza è minore vuol dire che questa volta la correzione sarà negativa. Il valore di dP è di 19. Si moltiplica quindi 19,4' per 19 e si ottiene con le tavole di moltiplicazione 19' x 0,19 = 3,6. Poi si aggiunge 0,4' x 0,19 = 0,1'. La correzione totale per l'angolo P vale quindi 3,7'. Abbiamo detto che tale correzione è negativa. L'altezza corretta dell'astro è quindi data da 64° 28,0' + 25,6' - 3,7' = 64° 49,9'. Cosa vuol dire questo valore? Confrontiamolo con l'altezza corretta della Luna che abbiamo ricavato dal sestante, 64° 59,6'. L'altezza della Luna da dove ci troviamo è leggermente maggiore che non dal punto stimato. Quindi ci troviamo nei pressi del punto stimato, ma un po’ più spostati in direzione del punto subastrale. Il valore di questa direzione è 194°, il valore della distanza dal punto stimato è di 64° 59,6' - 64° 49,9' = 9,7' ossia 9,7 miglia nautiche. Quindi il punto determinativo si trova partendo dal punto stimato 41° 0' N e 11° 0' E andando in direzione 194 gradi per 9,7 miglia nautiche. Da lì si traccia la retta di altezza, che avrà un azimuth perpendicolare, ossia di 104 / 284, valori praticamente identici a quelli trovati con la calcolatrice.
Il primo metodo
Si deve scegliere un punto stimato che abbia per latitudine un valore intero di gradi, come abbiamo appena visto per il secondo metodo, e per longitudine un valore tale che P abbia un valore intero di gradi. Quindi i valori dei primi e dei decimi di primo della longitudine del punto stimato devono essere uguali a quelli del punto subastrale; nel nostro caso, essendo l'angolo orario 355° 19,4' e quindi essendo la longitudine del punto subastrale 4° 40,6' E, sceglieremo un punto stimato il cui valore dei primi della longitudine sia di 40,6. Prenderemo in considerazione il punto di coordinate 41° Nord e 10° 40,6' Est. In tal caso P varrà esattamente 6 gradi. L'uso delle H.O.214 sarà così semplificato, ma si avrà qualche imprecisione grafica in più, in quanto il punto stimato sarà presumibilmente più lontano dalla realtà, in quanto scelto in base a considerazioni tabellari e non di navigazione reale. Un altro svantaggio minore del primo metodo risiede nel fatto che volendo tracciare più di una retta d'altezza sarà necessario utilizzare più di un punto stimato.
Il terzo metodo
Col terzo metodo non è più necessario scegliere un valore intero di gradi per la latitudine del punto stimato. Utilizzando le tavole per correggere l'altezza per la differenza di latitudine (sono poste immediatamente prima delle tavole di moltiplicazione, e funzionano con lo stesso principio) possiamo, per esempio, utilizzare come punto stimato le coordinate 40° 42,8' N e 11° 0' E. Per sapere poi se la correzione relativa alla differenza di 17,2' dal valore intero in gradi sia positiva o negativa sconsiglio vivamente di utilizzare lo specchietto riportato nella spiegazione del metodo all'inizio delle tavole: utilizzate piuttosto il ragionamento.
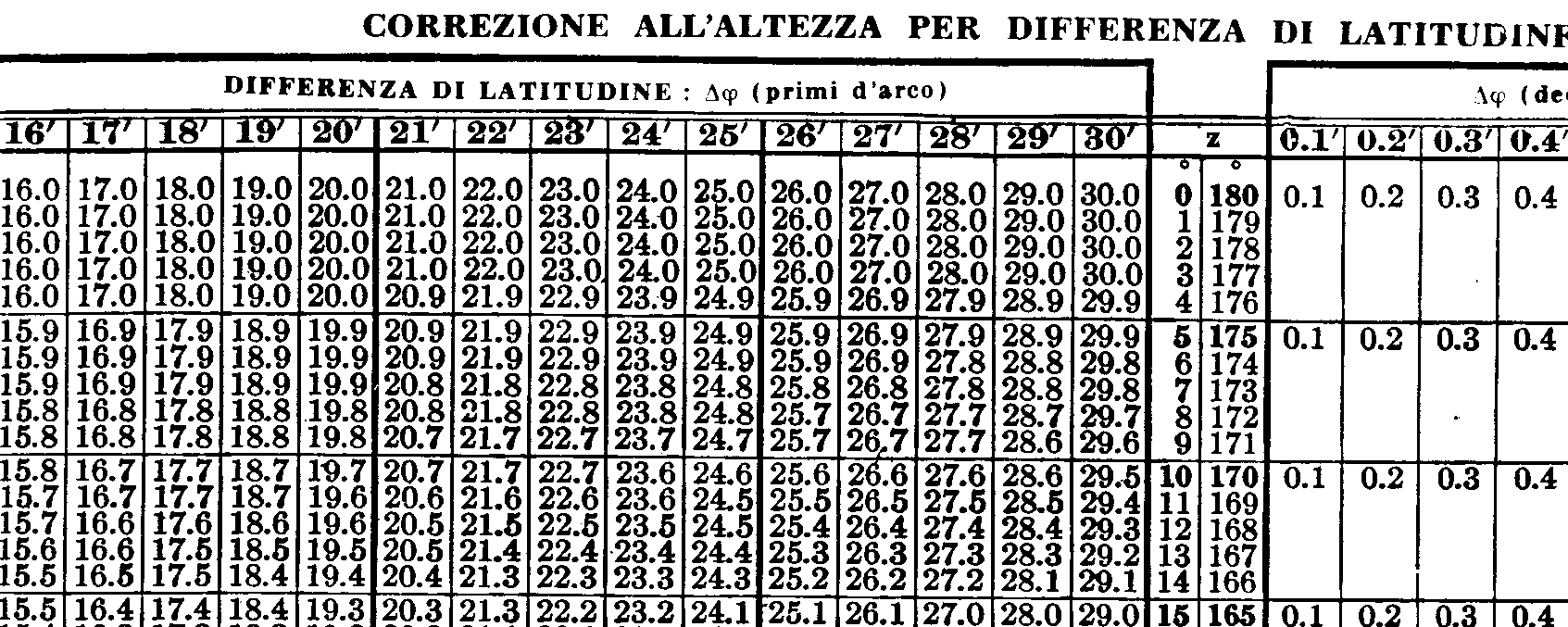
Dalle tavole ricaviamo che per Z = 166 la correzione per 17 primi è uguale a 16,5’ e che la correzione per 2 decimi di primo vale 0,2’. Quindi la correzione totale per la differenza di latitudine è 16,5' + 0,2' = 16,7'. Poiché un qualunque punto stimato posto a 41° 0,0’ N sarebbe a Nord del punto subastrale che abbiamo preso in considerazione, un punto di latitudine di 40° 42,8' N è senz'altro più vicino ad esso. L'altezza a cui appare la Luna è quindi maggiore. Tale altezza allora vale 64° 49,9' + 16,7' = 65° 6,6'. La distanza fra il punto determinativo ed il punto stimato di coordinate 40° 42,8' N e 11° E è quindi di 65° 6,6' - 64° 59,6' = 7,0 miglia nautiche. Il punto determinativo si trova cioè a 7 miglia nautiche dal punto stimato di coordinate 40° 42,8 N e 11° 0' E. Questa volta però l'altezza reale è più bassa dell'altezza dal punto stimato. Quindi il punto stimato è più vicino al punto subastrale. Per trovare il punto determinativo bisogna allora allontanarsi dal punto stimato in direzione opposta all'azimuth che va verso il punto subastrale: ci troviamo cioè nella situazione del secondo disegno del paragrafo "Come si trova la retta d'altezza". Quindi si parte dal punto stimato in direzione 014° per 7 miglia nautiche: lì abbiamo il punto determinativo da dove tracciamo la retta di altezza con direzione 104 / 284 gradi.
Giova ricordare che con i tre metodi possiamo arrivare a punti determinativi diversi, che possono essere tutti e tre corretti, in quanto tutti e tre appartengono al cerchio di altezza che ha centro nel punto subastrale.
Il terzo metodo è un po' più complesso, ma consente di utilizzare il punto stimato che si ritiene più opportuno, e che presumibilmente è quello più vicino alla realtà.